Pythagorean Theorem

Last updated on by Arikaran Kumar

Share0
Tweet0
Share0
Pythagoras-theorem

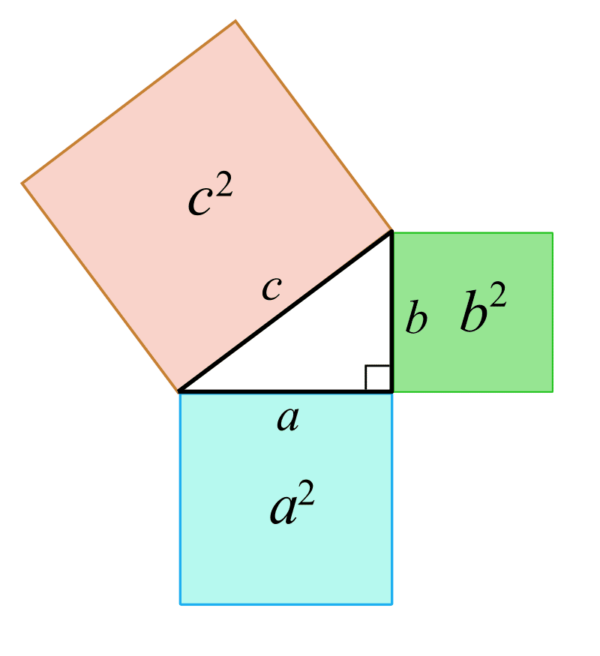
Image courtesy: wikimedia.org

In the previous blog, we learned about triangles and their properties as well as how to locate a triangle's area and a missing angle. This blog teaches us how to locate the triangle's missing side.

The Pythagorean Theorem, created by Pythagoras of Samos, can be used to solve for the missing sides of a right triangle. It states that the sum of the squares of the legs of the triangle is equal to the square of the hypotenuse.

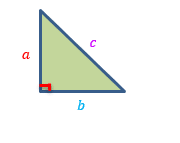
Pythagorean Theorem

Figure #1

Pythagorean Theorem

Figure #2

The theorem can be written as

a^2+b^2=c^2

Where a and b represent either of the legs, and c, the hypotenuse.

Using this theorem, the solution for each side can also be solved as

a=\sqrt{c^2-b^2}

b=\sqrt{c^2-a^2}

c=\sqrt{a^2+b^2}

Now that we have talked a bit about what the Pythagorean Theorem can be used for, let us examine at one of the many ways we can derive this formula.

Pythagorean Theorem Proof 

(Go To Table Of Contents)

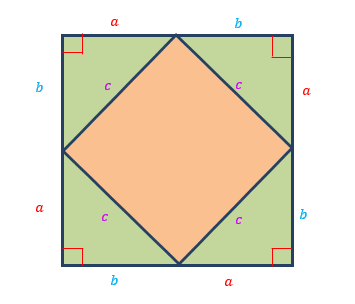
Pythagorean Theorem Proof

Figure #3

Look at Figure #3. We have a small green square inscribed in a larger beige square. The small green square has side lengths c. Since the green square is inscribed in the beige square, it creates 4 identical right triangles with the legs measuring a and b, and a hypotenuse measuring  c. Using this information, we can start creating equations to solve for each side of the right triangles.

Let’s first find the area of the beige square.

The area of a square is

A=l \times w

The length of the square is equal to a + b.

The width, since all sides of a square are equal, is also a + b. So,

A_{\text {beige }}=(a+b)(a+b)

Distributing, we get

A_{\text {beige }}=a^2+2ab+b^2

The area of the green square is

A=l \times w

A_{\text {green }}=c \times c = c^2

Next, let’s get the areas of the triangles. The area of a triangle is

A=\frac{1}{2} b h

Finding the area of one of the triangles, we can see that the base is b and the height is a.So, the area can be represented as

A_{\text {triangle }}=\frac{1}{2} (b) (a)

Since all 4 triangles are identical, we can obtain the total area of all four triangles by multiplying the area of 1 triangle by 4.

4 \times A_{\text {triangle }}=4 \times \frac{1}{2} (b) (a)

4A_{\text {triangle }}=2ab

Using this new information, we can form another equation for the total area of the beige square. We can add the areas of the 4 right triangles to the area of the green square to get the total area of the beige square.

A_{\text {beige }}=A_{\text {green }}+4A_{\text {triangle}}

A_{\text {beige }}=c^2+2ab

We now have two equations for the area of the beige square. We have

A_{\text {beige }}=a^2+2ab+b^2

and

A_{\text {beige }}=c^2+2ab

Now we can set both equations equal to each other and solve for c^2

A_{\text {beige }}=A_{\text {beige }}

a^2+2ab+b^2=c^2+2ab

Subtracting 2ab from both sides we get

a^2+2ab+b^2-2ab=c^2

Simplifying, we get

a^2+b^2=c^2

Now that we are done proving the Pythagorean Theorem, let’s apply it to some examples.

Book a Free Consultation Now!

To Learn more about Trigonometry tutoring at FPLA schedule a free consultation.

 Book Now !Free. Schedule A Call.

Examples 

(Go To Table Of Contents)

Find the missing side, x, of each given triangle

#1

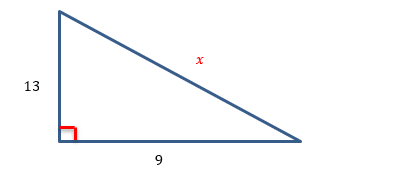
Figure #4

Figure #4

Remember:  

The Pythagorean Theorem states,

a^2+b^2=c^2

Where a and b are the legs and c is the hypotenuse.

Using the theorem, we can create the following equation for the triangle in Figure #4:

a^2+b^2=c^2

13^2+9^2=x^2

Simplifying, we get

169+81=x^2

250=x^2

Isolating  x we get

\sqrt{250}=\sqrt{x^2}

\sqrt{250}=x

\sqrt{25 \times 10}=x

\sqrt{25} \times \sqrt{10}=x

5\sqrt{10}=x

#2

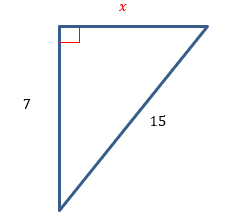
Figure #5

Figure #5

In Figure #5, we are missing the value of one of the legs of the triangle. To solve for x, we can create the equation:

x^2+7^2=15^2

Simplifying, we get

x^2+7^2=15^2

x^2+49=225

Isolating x we get

x^2+49-49=225-49

x^2=176

\sqrt{x^2}=\sqrt{176}

x=\sqrt{16 \times 11}

x=\sqrt{16} \times \sqrt{11}

x=4\sqrt{11}

Author: Mr. Vernon Sullivan, is a tutor at FPLA Miami, FL HQ premier 1-on-1 tutoring center. He teaches Algebra, Geometry, Pre-Cal, ACT, SAT, SSAT, HSPT, PERT, ASVAB and other test prep programs.

Mrs. Emimmal Sekar and Mr. Arikaran Kumar Proofread this article. Mr. Arikaran Kumar manages the website and the social media outreach. 

Equation of a Line
[Latexpage]How To Define Equation of a Line?By Robert OThe equation of a straight line has the standard form $$y=m x+c$$Where:m[...]
Read More 
How To Write Equations Of Perpendicular Lines
[Latexpage]How to Write Equation of a Perpendicular LineBy Robert OTwo perpendicular lines form an angle of 90o at the intersection[...]
Read More